数学作文（第四届数学文化征文）

本文为“2022年第四届数学文化征文活动

我眼中的数学思想

作者 : 刘瑞祥

作品编号：097

数学思想是一个很大的题目，论述的人很多，但是有的文章虽然以“数学思想”为标题，而内容却未必真的是数学思想，可能只是具体的解题方法。本文谈谈我眼中的数学思想。需要提前说明的是，这里只是我——一个普通数学爱好者——眼中的数学思想。

一、抽象化思想

最重要、最基本的数学思想就是抽象化。打从人类认识数字开始，就有了抽象化思想，可以说抽象在数学中无所不在，理应成为数学思想中的No.I。各种几何对象亦是抽象了的产物，比如点、线、面等等。尺规作图方面，直尺被抽象成无限长、无刻度的工具，圆规被抽象成脚距任意的工具，如此等等。进一步看，无论是集合，还是布尔代数，都是把研究对象尽量抽象，一直抽象到只剩一个字母作为躯壳而已。再比如欧拉对哥尼斯堡七桥问题的研究，也是把桥抽象成线，岛抽象为点的。抽象舍弃了与当下无关的次要因素，从而更深刻揭示事物的本质特征，展现出不同事物之间的共同点。而现代数学中的抽象早已超出了人类能直接想象的范围。

数学的抽象还影响到了其它学科。以力学为例，质点、质点组、刚体、弹性体等等就是客观实物不同程度的抽象。

二、确定性思想

自从数学诞生以来，数学问题的答案正误就像黑白一样分明。等于就是等于，不等于就是不等于。哪怕两者之间有着万亿分之一的差距，已经在现实中无法分辨，但在严格的数学上仍然是有区别的。这其中最佳例子就是圆周率，虽然现代数学已经可以计算出若干亿位数字，而它的精确表示方法仍然只是字母π。

说到这里我要补充一句，那就是伴随着现代数学的发展，好像这一思想已经变得过时了。不是有一本书就叫做《数学：确定性的丧失》吗？但在我这个低水平写手的眼里，这不过是一种误解，因为所谓“确定性的丧失”，其实是前提或者问题本身的变化而变化的。比如所谓非欧几何，因为前提（公设）和欧氏几何不同，所以才推出不同的结论。而要研究这些问题可能的结果，仍然需要数学。这正像工业化带来了环境污染，但要解决污染就要进一步发展工业。

三、公理化思想

说实话，这才是我第一个想到的数学思想，因为我毕竟是通读过《几何原本》的人。公理化方法其实基本就是逻辑法，在数学上的地位毋庸置疑，而其历史和意义我也不再重复。我只说一个问题：一般谈到公理化的人，往往会提到自洽性、独立性、完备性这三个特点。但从实用的角度来看，公理还应该具有简洁、方便的特点。比如三角形内角定理、勾股定理在一定程度上反映了平行公设，那为什么不以之代替平行公设呢？原因就在于不方便、不直观。

公理又是反直观的产物，因为如果把全部数学（当然这里的“全部”是指某个研究领域的“全部”）都归为公理的产物，那么这些公理必然是已经去掉了直观的表象，只剩下一堆逻辑命题。这当然对某些领域是有益的，比如机器证明，但对于人们的理解却是困难的。

四、算法化思想

我们在称赞公理化的同时，不应该忘记算法化思想，或者也可以称为“机械化思想”。不论这在古代是不是东方（中国）独有的思想，都无损于它独立于公理化思想的地位。它和公理化思想互相补充，相映成趣，宛如数学上的并蒂莲花。在数学上，凡是可以写成一定算法的内容，意味着具有简单、通用的解答方法，当然这个算法越简单就越好。比如用阿拉伯数字演算加减乘除，就比用罗马数字方便，再比如使用方程解应用题，就比直接列式容易，因为方程不但意味着多了一个条件（把未知量用字母表示出来），也意味着只要按照一定的程序，就可以得到结果。

在现代社会，算法更是得到了计算机的加持，可以发挥更大作用。我国数学家吴文俊、张景中等，深入挖掘算法思想，在机器证明领域做出了突出贡献。这充分证明了算法思想对现代数学的意义。

五、模型化思想

谈数学思想，不能离开模型化思想。比如前面提到的公理化思想中已经涉及非欧几何，而非欧几何的“合法地位”是和数学家建立非欧几何的模型分不开的。数学家适当修改了关于“直线”“平行”等概念的定义（或人们对之的印象），使得原来的平行公理不再适用。当然模型对几何基础的功劳不止于此，比如普通的四面体就可以看作是某些公理的一个模型：它满足两点（这里的点仅指“顶点”）确定一直线、两线交于一点等公理。

实数论把实数和直线上的点对应起来，从而使得实数有了坚实的基础。而复数则是模型化的又一个例子。平面上的点和复数建立一一对应的关系，这以后就可以用平面上点的坐标研究复数了。类似的，高维空间超出了人类直觉把握的能力，如何研究？方法很简单，就是用列（或行）向量作为其模型，使高维空间的点和一组实数对应起来。

六、转化思想

数学上的转化无处不在。最初等的比如把应用题中的条件转化为式子，高级一点的比如把数量关系转化为图形。适当的转化往往可以简化问题，为我们最终解决问题提供一个良好的途径。比如，设a,b,c,d均大于0且a/b<c/d，则可证a/b<(a+c)/(b+d)<c/d。这个问题虽然可以借助字母进行推理，但无论如何不如转化为斜度、平均速度等问题来得直接、清楚。而式子

更需要借助类似于下面的图来证明。

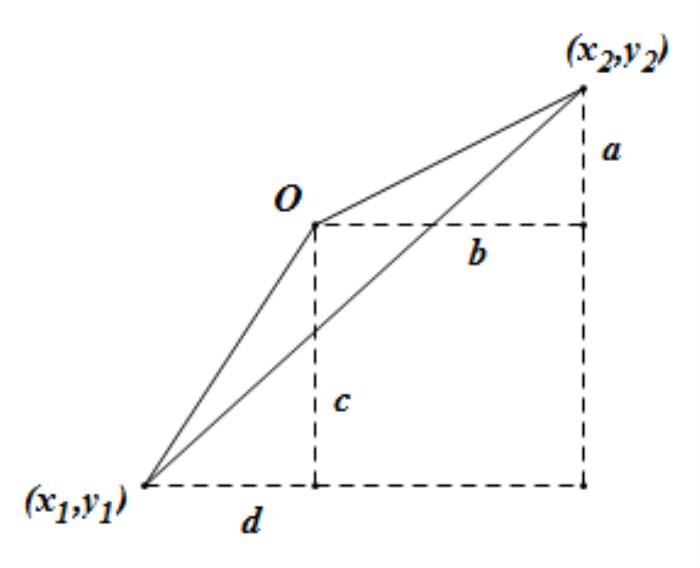
再举几个转化的例子吧。比如怎样得出平行四边形面积公式？方法便是将其转化为长方形。而几何中更常见的是各种数量关系和图形位置的转化，比如要证明平行，可证明同位角相等，反之亦然。反证法也是转化的例子，如果你无法直接证明，可以证明结论的反面不成立。

前面提到的模型化思想，似乎也可以称为转化思想，但二者在本文中的区别是，模型化指的是更“基本”的方面，往往针对一个数学领域，而“转化”则是针对具体的数学问题。

七、极限思想

极限是微积分的基本概念，而微积分在现代数学中的地位是无可置疑的。众所周知的是，极限概念经过几代数学家的努力，终于有了一个坚实的基础。由此，微积分才成为一个可以放心使用的工具。

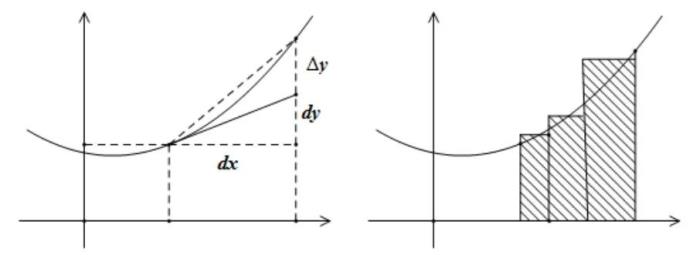
在几何上，极限有几个重要应用：首先是割线的极限为切线，其次是利用极限方法求面积和体积。这正是微分和积分的源头。然而微积分一旦产生，就冲出数学界，成为各个领域的有力工具，这甚至早在极限概念严格化之前就发生了。

愈是重要的就愈难用语言描述。关于极限，就说到这里了。

八、恒定思想

只有真正永恒的才是有价值的。这句话虽然是杨振宁先生为怀念邓稼先而写的，但同样适用于其它领域，比如数学。在数学上，有意义的是某种变换下不变的量。以欧拉定理为例，V-E+F=2，这个常量2就是一个重要的不变量，它揭示了不同的简单多面体之间的联系。如果引入“体数”S，则上式可以写作V-E+F-S=1，这里各字母依次是点（零维）、棱（一维）、面（二维）、体（三维）。不但如此，对于一维图形，由二点一线组成，二维简单图形则是n点n线，均满足后者。射影几何中，也有很多重要的不变量（不变关系），比如交比、结合性等。

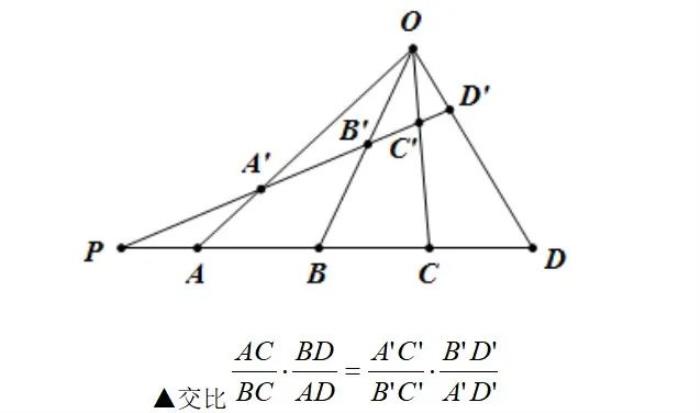
在解方程（不等式）的过程中，需要保持每一步变形都是同解变形，如果遇到可能产生不同解的操作，则需要验根。

关于这一思想，我要说明的最后一点是，这个思想的名字是我自己起的，因为我没有找到合适的专有名词。

欢迎读者的补充和讨论。

已发文章>>

001 阅读《数学的故事》有感

002 我想和数学谈场恋爱

003 数学“化错”中的美

004 让数学思考成为数学课堂的主旋律

005 卢梭的“错”？

006 数学教学案例《找次品》

007 基于优化学生数学思维的高效课堂创建——以等腰三角形的判定一课为例

008 从特殊到一般，引导数学思维

009 数学文化融入家庭教育的研究

010 sin 震荡函数的图像分析

011 四阶幻方的“太极图”性质

012 无理数的定义和实数理论的建立

013 一个容易被忽视的问题——数学文化

014 “双减”背景下初中数学学科的合作学习方式探究

015 中学数学德育渗透的方法与路径

016 《数学的力量》读后感

017 基于数学文化的单元统整教学设计——以“圆的认识与面积”教学为例

018 有助于数的理解的数字圈环

019 以折叠为例，探究生长型数学教学模式

020 我从事数学科普写作的经验与启示

021 在阅读中滋长智慧——读《教育智慧从哪里来》有感

022 学习数学史 做数学的使者

023 开数学文化之窗 启数学文化魅力——阅读《美丽的数学》有感

024 “文学独白”——数学教学因你而精彩

025 如何用多面体三等分正方体

026 HPM视角下《圆的周长》教学设计

027 被误解的“勾股定理”

028 好玩的数学

029 帮小青蛙设计一个井

030 万物的基础——数学——读《从一到无穷大》有感

031 读《孙子算经》鸡兔同笼问题有感

032 HPM视角下高中数学多样化作业的设计

033 攀越高峰的领路人——数学文化

034 我的好兄弟：数学

035 细嗅数学文化之香

036 藤蔓的喜悦

037 物理力学中数学的影子

038 复数外传

039 函数的历史和发展

040 数学文化与我

041 数学之趣

042 探索数学知识背后的秘密

043 数学文化和我的数学学习

044 古代算数几何形体——阳马与鳖臑

045 数学文化与我的数学学习

046 我与数学文化

047 “形象”的数学

048 站在巨人的肩膀上学习数学

049 从数学文化和个人影响的角度剖析对数的历史

050 论数学文化

051 我与数学文化

052 正弦定理的源起与应用

053 数学文化融入初中数学教学的实践与思考

054 给数字爱好者的1个全新的0至9数字思考挑战及应用问题

055 并不需要的“承重墙”与数学课改中的问题 —— 兼与马立平博士商榷

056 奇妙的规律

057 生活中的“家常便饭”——数的表示方法

058 读《黄东坡智慧大讲堂——带你发现数学之美》有感

059 通识教育视角下初中数学思维培养从直观向抽象过渡的研究

060 读《古今数学思想》有感

061 为什么圆的面积的导数等于周长？球的的体积的导数等于其表面积？

062 《奇妙的数学文化》读后感

063 数学文化视角下《九宫图的奥秘》教学设计

064 关于毕达哥拉斯定理适用蒙特卡罗方法验证的探讨

065 遨游数学星空，体味数学奇妙

066 核心素养下的，数学文化中的美育渗透

067 探寻数学之奇，欣赏数学之美

068 框架思维——读《数学这样学就对了》有感

069 从肌肉记忆到《几何原本》第四公理

070 《数学大世界》读后感

071 除法才是四则运算的基础：兼与马立平博士商榷

072 从“海盗分金”到“囚徒困境”——博弈该如何进行？

073 “0”与“1”的辩证法和数学学习之路

074 感悟数学

075 我的好伙伴：数学

076 一则寓言故事带来的教学启发

077 神奇的数学 ——最大公因数、最小公倍数

078 怎样学好数学

079 “7”真是个神奇的数字

080 《一个定理的诞生：我与菲尔茨奖的一千个日夜》读后感

081 梦想中的职业，都与数学息息相关

082 哪⾥有数，哪⾥就有美⸺读《数学之美》有感

083 探索信息技术融入初中数学文化实践活动

084 秦九韶数学案——随机抽样统计推理的反问题

085 第四次数学危机

086 基于三阶魔方的STREAM教学设计

087 趣味家庭作业 引领学生学习

088 数学之道

089 了解微积分后的那些事……

090 不会？不，会

091 一个偶然的发现——完全数及其基因构造数列

092 在规矩方圆中求索——“圆的认识”的文化育人视界

093 欧拉公式的几何证明与意义

标签：